Estatica
La estática abarca el estudio del equilibrio tanto del conjunto como de
sus partes constituyentes, incluyendo las porciones elementales de
material.
Uno de sus principales objetivos es la obtención de
esfuerzos cortantes, fuerza normal, de torsión y momento flector a lo
largo de una pieza, que puede ser desde una viga de un puente o los
pilares de un rascacielos.
Momento
El momento de una fuerza se calcula como el producto vectorial entre
la fuerza aplicada sobre un cuerpo y el vector que va desde un punto
"O" (por el cuál el cuerpo giraría) hasta el punto dónde se aplica la
fuerza.
El momento de una fuerza se calcula como el producto vectorial entre
la fuerza aplicada sobre un cuerpo y el vector que va desde un punto
"O" (por el cuál el cuerpo giraría) hasta el punto dónde se aplica la
fuerza.
El módulo se calcula como:
M = F d sen θ
F = Módulo del vector fuerza
d = Módulo del vector distancia
θ = Angulo entre los dos vectores trasladados al origen
Palanca
Se
trata de una máquina simple formada por un elemento rígido en dónde se
encuentran la potencia, la resistencia y un punto de apoyo. Debido a que
la suma de los
momentos es cero, permite mover objetos pesados haciendo menos fuerza.
P a = R b
Consideramos a P y a R como vectores paralelos, tal como en la posición horizontal de la palanca.
Palanca de primer grado
Es
importante tener en cuenta que el punto de apoyo no necesariamente
tiene entre la potencia y la resistencia. Puede estar también en uno de
los extremos como en los demás grados de palanca.
Polea fija
En
las poleas fijas, las tensiones (fuerzas) a ambos lados de la cuerda
son iguales (T1 = T2) por lo tanto no reduce la fuerza necesaria para
levantar un cuerpo. Sin embargo permite cambiar el ángulo en el que se
aplique esa fuerza y transmitirla hacia el otro lado de la cuerda.
Polea móvil
Con cuerdas paralelas y verticales
En
las poleas móviles la fuerza para lograr el equilibrio la fuerza se
divide por dos siempre y cuando las cuerdas estén verticales (sin formar
un ángulo)
- P = T1 + T2
T1 = T2
Por lo tanto la tensión para mantenerlo en equilibrio es la mitad del peso
Con cuerdas no verticales
Si
en cambio tenemos un ángulo entre las cuerdas planteamos el equilibrio
descomponiendo las fuerzas en X e Y. La sumatoria de fuerzas en cada eje
debe ser igual a cero.
Plano inclinado
El
plano inclinado es una máquina simple que permite subir objetos
realizando menos fuerza. Para calcular la tensión de la cuerda que
equilibra el plano, descomponemos las fuerzas y hacemos la sumatoria
sobre cada eje. Es recomendable girar el sistema de ejes de tal forma
que uno de ellos quede paralelo al plano. Con esto se simplifican las
cuentas ya que la sumatoria de fuerzas en X tiene el mismo ángulo que la
tensión que lo equilibra.
Torno
El
torno es una máquina simple formado por un cilindro y una manivela, que
permite levantar un cuerpo pesado haciendo menos fuerza.
Problema 1: determinar la resultante de las 2 fuerzas indicadad en
la figura, dando el modulo y el angulo que forma con la horizontal.
La resultante es la suma de las 2 fuerzas.
SOLUCION: de la ley del coseno se obtiene f= raiz cuadrada de 300x300 + 400x400 +2x300x400xcos de 60
de la ley del coseno se obtiene: sen a/300 = cos a/608 ----> sen a = 04273
a= 25,3º
SOLUCION EN COMPONENTES:
la resultante es la suma de las componentes de cada una de las fuerzas
F=400i + 300x(cos 60i + sen 60j) --->F=550 + 150x raiz cuadrada de 3
tan a = 150 x raiz cudradrada de 3 =04723 ---> a= 25,3 º
2)Sabiendo que la siguiente escalera (m = 15 Kg) no desliza, encuentre el ángulo entre la reacción "R" y el suelo.
en un punto 
en un instante dado dependen sólo de las deformaciones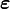 
en el mismo punto y no de las deformaciones anteriores (ni el valor de
otras magnitudes en un instante anterior). Para un sólido elástico la 
denota el conjunto de tensores simétricos de segundo orden del espacio
euclídeo. Si el sólido es homogéneo el valor de la función anterior no
dependerá del segundo argumento.
